Noon last Thursday, I counted 14 sentient beings on a three-mile stretch of Samoa Beach. Dogs count as sentient, of course; seabirds don’t, not so obviously. The guv’s talking about closing all California beaches. I hope it doesn’t happen, but can understand the reasoning — close off beaches in the south of the state, leave ours open, and anarchy ensues. I get it.

[Ed. note: As is probably apparent, this was written a few days ago. This is what did happen, though anarchy did not ensue.]

Instead of going on a rant about C-19 and the mish-mash of rules and regs being enacted to deal with it, it’s the number five I want to celebrate, brought on by this little sand dollar I found there. Alive, these lovely echinod creatures—basically, flattened sea urchins—are purple; dead, they’re white. Their most obvious feature is the five-fold radial symmetry of their “petals.” In South Africa, the flower analogy gives them the name “pansy shells.” Starfish, to which sand dollars are related, have five arms (pentamerism). In fact, look around at nature, and you’ll see five everywhere.

The place to start, of course, is with our own fingers and toes. I’m particularly aware of this as I type. I was a two finger hunt-and-peck typist most of my life, but some years ago I determined, if I was really going to think of myself as a science writer, it was time to learn to touch-type. Which I did, by sticking little squares of Band-Aid over the keys. I’ll never be a good typist, but at least I use all the digits on both hands, never — well, hardly ever — glancing down at the keyboard.

Five is such a cool number. I remember my delight when reading what the late Martin Gardner (who wrote the “Mathematical Games” monthly column in Scientific American for a quarter of a century) pointed out, that not only were there exactly five “Platonic solids,” but that even an all-knowing, all-powerful God couldn’t change that. A Platonic solid, if you’ve forgotten from school, is a symmetrical polyhedron whose faces are made up of regular polygons —triangles, squares and pentagons. Thus, fair dice can only be Platonic solids, where you can have four, six (normal dice), eight, 12 or 20 faces.

(The “five” proof is easy. Imagine looking straight down at a vertex, where the polygons meet. At least three meet for it to be a solid. And there can’t be more than five, since with six, you’d have a flat surface, like the cells of a honeycomb. So three, four or five — I’ll leave it to you to figure out the only five possible polyhedrons from there.)

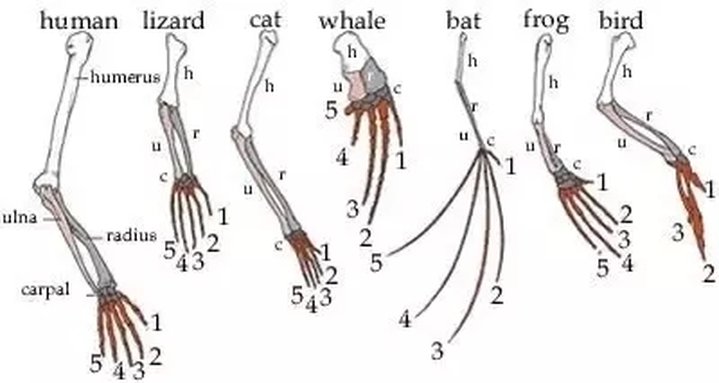
Virtually all mammals, reptiles and amphibians have five digits, which means that the five-fold pattern evolved before these groups diverged 340 million years ago. From fossil evidence, we know that nature had been having a gay old time before then, experimenting with tetrapods (four-limbed animals) having six, seven and eight digits. An evolutionary “rule” says that it’s easier to lose something than to regain it, so maybe the five-plus digital creatures lost their “additional” digits, down to five. But, for reasons paleontologists don’t really understand, nature stopped there. Apparently five conferred some evolutionary advantage that four didn’t.

I could wax lyrical about five: senses, pillars of Islam, books in the Torah, classical elements (earth, fire, water, air, ether), the Freemasonary pentagram, naked eye planets (hence seven days of the week, with the sun and the moon), the perfect fifth (in Western music), the Olympic games flag (the rings representing the continents), Chanel Number 5…

But I won’t.