After scrivening this column for over seven years (this is #379) I thought I had a pretty fair idea of which of them would elicit a “meh” reaction and which – GMOs and UFOs, for instance — would bring out the critic that lives inside all of us. Wrong again. A couple of weeks ago, I wrote about probabilities — how much more mundane a topic can you get? To my surprise, a ton of folks responded. Many of whom made my point for me, that we tend to rely too much on our gut feelings (“That can’t possibly be true!”) than on basic-but-boring logic. So much so that I think it’s worthwhile revisiting it, with my very best effort at explaining why the (non-intuitive!) solutions I gave are correct. And — bonus! — Monty Hall.

Urn Problem

You’re shown two urns, one of which contains one black and one white ball; the other contains two black balls. You pick one urn at random and put your hand in, pulling out one ball: it’s black. What’s the probability that the second ball in that urn is also black?

2/3.

Label the balls B1 and B2 (in one urn) and B3 and W1 in the other. You’ve pulled out, with equal probability B1, B2 or B3. In two of those cases (B1 and B2) the other ball is black, while in one of those cases (B3), the other ball is white.

Mitch’s ATM Puzzle

An ATM dispenses $20 bills and has only four left, one of which is a counterfeit. Alice and Bob and Carol and Dave each make a $20 withdrawal from the ATM, after which it has no money left to dispense. You decide to check the women’s bills first, starting with Alice. Alice does not have the counterfeit. What are the odds that Carol will have the counterfeit?

1/3

This is the urn problem revisited. After Alice has checked her bill, we’re left with three bills, one of which is counterfeit, so the odds of either Bob, Carol or Dave getting it are one in three. Which brings us to…

The (Notorious) Monty Hall Puzzle

Both the urn and the ATM teasers have echoes in what’s become known as the “Monty Hall puzzle,” after the late Monty Hall, host of Let’s Make a Deal for many years. In fact, several commentators of two weeks ago brought it up.

To remind you of the set-up: Monty gives you the choice of three doors: behind one door is a car; behind the other two, goats. You pick a door, say No. 1, and Monty, who knows what’s behind the doors, opens one of the other doors, say No. 3, revealing a goat. (He never opens the door hiding the car, of course.) He says to you, “Do you want to switch and pick another door?” The gut reaction of most people is no — there’s a 50/50 chance that either of the two closed doors hides a car, so whether you switch or not is immaterial.

When Marilyn von Savant wrote, in her regular Parade magazine column, that yes, switching improves your chances of winning the car, ten thousand readers (including many math professors!) took her to task. “How could switching doors possibly make a difference?” they asked. “You either picked the right door or you didn’t, and the fact that one of the doors is now open doesn’t change that!” But it does.

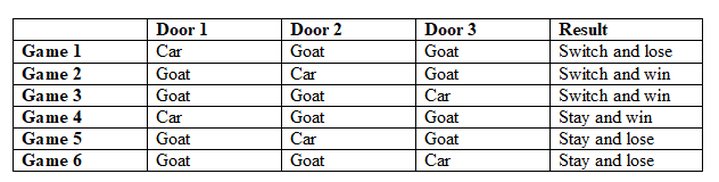
Take a look at this matrix, which exhausts all possibilities for when you pick door No. 1 and Monty opens a door hiding a goat. If you switch (games 1, 2 and 3), you increase your chance of winning the car to 2/3 compared with 1/3 if you stay (games 4, 5 and 6).

Birthday ‘Paradox’ Re-explained

How come the odds of two people in a group of 23 sharing the same birthday are better than 50/50?

If two people meet and exchange birthday dates, the odds of them sharing the same date are 1 in 365, so the odds of them not sharing the same birthday are 364 in 365.

In a room of 23 people, how many pairs of people have to check with each other to see if they share the same birthday? It’s the same as the number of handshakes, assuming everyone shakes the hand of everyone else. The first person to go shakes hands with 22 people; the second with 21 (having already shaken #1’s hand); the third with 20, etc. Total number of handshakes/pairs, is then 22 + 21 + 20 +…+ 1 = 253.

With 253 pairs, the odds of two people in a group of 23 not sharing the same birthday are 364/365 multiplied* by itself 253 times, i.e. (364/365)^253, which Google tells me is a tad less than 0.5. So the odds that two people in the room do share a birthday are better than 50/50.

* Note that each pairing is independent of all the others, so you multiply the odds. It’s like tossing a coin: toss it three times and the odds of getting three heads are ½ x ½ x ½, or one eighth. Your turn: Flip a coin four times. (1) What are the odds of getting three heads and one tail in that order? (2) In any order?