Tired of Covid? Yeah, I get it. So what else is happening on the Internet? Well, weirdly, this little math problem keeps popping up on my feed, in one or another version. It’s simple to pose, but gives two presumably valid answers, with each camp firmly convinced of their rightness and the other side’s wrongness:

6 ÷ 2(1 + 2) = ?

Take a moment, if you haven’t already done so, to answer.

Did you get 1 or 9?

If you got 1, you’d have used the implied “juxtaposed multiplication” rule. We can all agree that (1 + 2) = 3, so you then multiply that by the 2 that’s juxtaposed with (i.e. sitting right outside of) the parentheses. Now you have 6 ÷ 6 = 1. Thus:

6 ÷[2(1 + 2)] = 1

Getting 9 depends on PEMDAS, which you may have learned in school as “Please Excuse My Dear Aunt Sally.” It’s the order in which you were probably taught to calculate an expression: Parenthesis, Exponents, Multiplication, Division, Addition, Subtraction. Except you should really have been taught PEMA, since multiplication and division are one and the same operation (dividing by 3 is identical to multiplying by its inverse, 1/3) and subtracting 5 is identical to adding –5.

Using PEMA on the above, you get:

1. Parenthesis: Calculate (1 + 2) to get (3)

2. Exponents: None

3. Multiplication. The PEMA rule says: complete multiplication/division operations in the order in which they occur from left to right. So we first do 6 ÷ 2, i.e. 3, then do 3(3) = 9. Thus:

[6 ÷2](1 + 2) = 9

So the problem boils down to, what order of operations are you supposed to use? If you follow what I think of as the “natural” process, you’ll end up with 1, while a strict reading of PEMA gets 9. The problem is that the problem is ill-defined, and should never be asked in, say, a SAT or GRE exam. Instead, it should be set with appropriate use of brackets, as I’ve added above. For what it’s worth, Google turns the original expression into (6 / 2) * (1 + 2) to give 9.

A similar ambiguity crops up, for instance, with the expression 5/5/5/5, which again should never appear “naked” like this, since it can reduce to 1, 1/25 or 25, depending on the order in which each / is applied. For instance, (5/5)/(5/5) = 1, while 5/((5/5)/5)) = 25. Like 6 ÷ 2(1 + 2), the expression 5/5/5/5 is ill-defined.

Some of the confusion may have arisen with the six-hundred year history of the division sign, which can take ÷ (the obelus, as used in this puzzle), / the solidus or slash, : (the colon, e.g. “a slope of 2:1”), ) (a curved bracket, as used, perhaps, in your first grade division practice); and a vinculum, or horizontal line, with the numerator above and denominator below.

If the original question had been posed with a vinculum instead of an obelus, it would have been unambiguous:

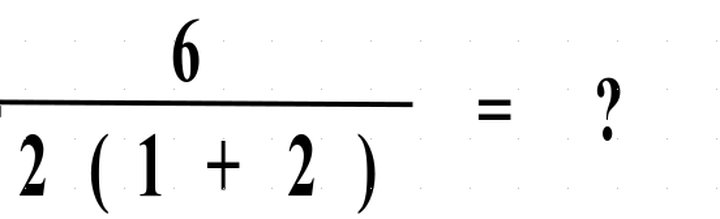
As I say, the curious thing, if you’ve seen this on the Internet and read the comments, is how attached each side is to their point of view—if you picked “1”, anyone claiming that “9” is correct is obviously an idiot. And vice versa.

It reminds me of the ongoing debate about using “they” and “their” with singular nouns, as I did above. Is it OK to say, “Any student handing in their homework late will be penalized”? (As opposed to the clunky “his or her homework” or the sexist “his homework”.) “If anyone arrives early, they must wait outside”—is that kosher? Battle lines have been drawn and, whichever camp you align with—“Yes, it’s fine!”, or “No, never!”—you’re right, dammit, and the other side is wrong.

Could we just agree to differ and, you know, give peace a chance?